A matematika-filozófiai formalizmus találkozása az elme-filozófiai fizikalizmussal

E. SZABÓ LÁSZLÓ
MTA-ELTE Elméleti Fizikai Kutatócsoport
ELTE Tudománytörténet és Tudományfilozófia Tanszék

 

Absztrakt: Jelentés nincs. Intencionalitás nincs. A dedukció indukció.

A MATEMATIKA FILOZÓFIÁJÁNAK centrális problémája, hogy hogyan definiáljuk a matematikai igazságot, vagyis, hogy mi teszi a matematikai állításokat igazzá?

A REALIZMUS szerint a matematikai állítások akkor igazak, ha megfelelnek a minket körülvevõ fizikai valóságnak. Más szóval, a matematika empirikus tudomány: a matematikai állítások a fizikai világ legáltalánosabb tulajdonságait fejezik ki. E felfogás fontos szerepet töltött be a matematika történetében, manapság azonban senki sem gondolja komolyan, hiszen a matematika fogalmai nincsenek közvetlen megfelelésben a valóság elemeivel, például a végtelen fogalmának semmi sem felel meg a külsõ (a matematikán kívüli) világban. Úgy, ahogyan ezt érteni szokás, elvetjük tehát azt a tézist, hogy ,,a matematika empirikus tudomány'', jóllehet végsõ konklúziónk szerint - mint látni fogjuk - az. Mint ilyen azonban nem a fizikai világ legáltalánosabb, hanem, épp ellenkezõleg, nagyonis partikuláris, és önmagában véve érdektelen tulajdonságait fejezi ki.

A MATEMATIKAI PLATONIZMUS a matematika klasszikus fogalmainak önálló létezést tulajdonít , függetlenül attól, ismerjük-e azokat, vagy nem, s úgy véli, a matematikai állítások igazságát pusztán e fogalmak analízisével, logikai úton láthatjuk be. A platonista számára nem probléma egy számot úgy definiálni, hogy ,,l a legnagyobb olyan prim, melyre l-2 is prim, vagy l=1, ha ilyen szám nem létezik.'' A platonista Gödel számára nem okoz gondot egy formális rendszerben ,,nem bizonyítható mondatok halmazáról'' beszélnie, s azt ,,konzisztencia'' címen összevetnie az ,,igaz'' mondatok halmazával.

AZ INTUICIONISTÁK tagadják a matematikai objektumoknak - az értelemszerûen véges - konstrukciójuktól független létezését, s azt a szót ,,végtelen'' legszívesebben kitiltanák a matematika szótárából, ám helyette ,,saját istenük'' (Curry kifejezése ¹ ), az Intuíció létezésében hisznek, vagyis valami olyasmiben, ami az egyetemes emberi értelem számára a priori adott, garantálva ezzel a matematika objektivitását és használhatóságát.

REALISTÁK, PLATONISTÁK ÉS INTUICIONISTÁK mind hisznek azonban abban, hogy a matematikai állításoknak jelentésük van, s ha - a Hilbert-programot követve - formalizáljuk is a matematika nyelvezetét, azt azért tesszük, hogy e jelentést precízebben és tömörebben adhassuk vissza.

A történet többi része jól ismert: a realizmus - mint már említettük - meghalt akkor, amikor elvágtuk a matematika és a valóságos fizikai világ közötti köldökzsinórt, a platonizmus a Gödel-tételeivel küszködik (Eszterházyval szólva, ,,ha minden állításról el tudjuk dönteni, hogy hamis-e vagy igaz, akkor ott valami nincs rendben''), az intuicionisták pedig már a matematika testét amputálják.

A MATEMATIKA FORMALISTA FELFOGÁSA szerint - legalábbis a formalizmusnak az itt proponált radikális változata szerint - az igazság ezzel szemben az, hogy a matematikai objektumoknak nincs jelentése. A matematika a formális rendszerek tudománya: Jeleket definiálunk és szabályokat , melyek alapján e jeleket kombinálhatjuk. Ez minden. A matematikának semmi köze nincs a végtelen metafizikai fogalmához. A matematika nem produkál, és nem old meg Zénon-paradoxonokat! A matematika éppolyan közömbös a végtelen fogalmával szemben, mint a térre, idõre, valószínûségre vagy a folytonosságra vonatkozó intuiciónkkal szemben. ,,Leírhatok egy jelet, mondjuk 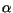-t, és elnevezhetem az egész számok kardinalitásának. Aztán rögzíthetem a rá vonatkozó manipulációs szabályokat'', mondja Dieudonné ² . Az egész finitista próbálkozás felesleges. Ha a papírra azt írom 10¹⁰¹⁰, ez éppúgy csak egy jel, amellyel manipulálhatok, mint bármelyik más.

Olyan ez, mint a sakk. Adottak a szimbólumok és adottak a játékszabályok. Minden lejátszott parti egy bizonyított tétel. A dedukció tehát egy kombinatorikus, mondhatni mechanikus játék.

A FORMÁLIS RENDSZEREK ONTOLÓGIÁJA kristálytiszta: a jelek, mondjuk papír-molekulák közé diffundálódott tinta-molekulák, pontosabban azok kölcsönhatása a megvilágítást jelentõ elektromágneses mezõvel, vagy valami ilyesmi. A szabályok, a mechanizmus, melyek szerint ezek a jelek a papirosra íródnak, szintén jól értelmezhetõ fizikai folyamatok, fizikailag kódolt, vagy kódolható szabályszerûségekkel. Persze a papíron történõ levezetés kicsit olyan, mint egy olcsó munkaerõt foglakoztató gyárban a gépsor, ahol a gyártási folyamat bizonyos pontjain emberi kéz (+ agy) teszi át a munkadarabot egyik futószalagról a másikra. De ez csak technikai kérdés, megoldható lenne komputerekkel, vagy jól idomított állatokkal, stb. A jelek is lehetnek egészen más természetûek, lehetnek egy komputer elektronikai állapotai, melyeket konkrét, alattuk végbemenõ fizikai folyamatok testesítenek meg,

FEJBEN is elvégezhetünk levezetéseket. Ha a formális rendszer szimbólumai és szabályai a legkülönbözõbb fizikai állapotokban (folyamatokban) testesülhetnek meg, miért ne testesülhetnének meg az emberi agy neuro-fiziológiai, biokémiai, biofizikai, röviden fizikai konfigurációiban, pontosabban fizikai folyamataiban. Ha ez így van, ha a ,,biztos tudás'' - egyes racionalisták szerint egyedüli - forrását jelentõ deduktív/logikai gondolkodás értelmezhetõ tisztán fizikalista keretek között, ráadásul mindenféle ,,jelentés'', ,,intencionalitás'', a fizikaira történõ lokális ráépülésen (local supervenience) túlmutató, akauzális, globális ráépülésre (global supervenience)³ való - részben homályos, részben tarthatatlan - hivatkozás nélkül, akkor ez egy kitûnõ érv a fizikalizmus mellett.

,,REPREZENTÁCIÓ'', ,,FORDÍTÁS '', ,,MEGÉRTÉS'' az a három szó, melyek használatát szándékosan kerüljük. Egy formális rendszer, a maga konkrét fizikai mivoltában teljes, mûködõképes, hasznos és metafizikailag értelmezhetõ. Nincs szükség annak feltételezésére, hogy ,,reprezentál'' valamit. Ez szükségtelen visszatérést jelentene a matematika realista, platonista vagy intuicionista felfogásához. Minthogy egy formális rendszer nem reprezentál semmit, nem lehet arról szó, hogy különbözõ formális rendszerek valami közös dolognak különbözõ reprezentációi lennének, tehát nem ,,fordíthatók''. Az egyik rendszer nem ,,érti'' a másikat.

(KÖLCSÖN)HATÁS a megfelelõ fogalom a reprezentáció, fordítás és megértés helyett. Ez az, ami a valóságban megtörténik. Két formális rendszer, mint két konkrét fizikai objektum közötti fizikai kölcsönhatás. Wittgenstein talán a nyelv használatának nevezné az agynak más formális rendszerekkel, mindenekelõtt más agyakkal - általában közbülsõ formális rendszereken keresztül megvalósuló - kölcsönhatását. Nem nominalizmusunk tart vissza attól, hogy e kölcsönhatások mögé, valamiféle ,,reprezentált jelentés fordítását és megértését'' képzeljük el, egyszerûen másról van szó. Ontológiailag semmi különbség nincs a között, ha az egyik matematikus a másik által leírt matematikai bizonyítást olvassa, vagy ha a kutyámnak felolvasom a Háború és békét.

AZ INDUKTÍV KÖVETKEZTETÉSSEL szemben gyakori kifogás, hogy egy általános kijelentés igazsága nem bizonyítható teljes bizonyossággal, annak empririkus tesztelése útján. Abból a tapasztalatból ugyanis - hangzik az érv -, hogy tetszõleges n számú esetben valami igaznak bizonyult, nem következik, hogy az n+1-ik esetben is igaz.

Meg kell azonban kérdeznünk, milyen értelemben ,,nem következik''?... És milyen értelemben ,,következne'', ha következne? A deduktív következtetés értelmében, logikailag - hangzik a szokásos válasz. A dedukció, az indukcióval szemben, ,,bizonyosságot'' nyújt.

A osztható 2-vel
A osztható 3-mal
A osztható 4-gyel

A osztható 12-vel

Ez a tisztán gondolkodás útján nyert konklúzió biztos, és/mert nem támaszkodik a tapasztalásra, a világ empirikusan megismert tényeire - mondják.

A RACIONALIZMUS kiinduló pontja éppen ez: a gondolkodás tudásunk egyik független forrása, sõt sokkal megbízhatóbb forrása, mint a tapasztalás - mondják -, hiszen a szükségszerûen igaz tudásának forrása a gondolkodás és nem a tapasztalat.

Tegyük most félre az induktív következtetés útján nyert tudás episztemológiai értékelését, és foglalkozzunk továbbra is a dedukcióval. ,,A matematikai és formális-logikai igazságokkal kapcsolatban az empirizmus nehézségekbe ütközik'' - írja Ayer. ,,Mert amíg a tudományos általánosítás esetében elismerten fennáll a tévedés lehetõsége, addig a matematikai és logikai igazságok mindenki számára biztos és szükségszerû igazságoknak tûnnek. De ha az empirizmus helyes, akkor egyetlen olyan állítás sem lehet biztos és szükségszerû, amely a világ tényeire vonatkozik. Ennek megfelelõen egy empirista a következõ két módon viszonyulhat a logikai és matematikai igazságokhoz: vagy azt mondja, hogy azok nem szüségszerû igazságok ..., vagy azt, hogy nem a világ tényeire vonatkoznak .... Ha egyik kurzus sem válik be, kénytelenek vagyunk utat engedni a racionalizmusnak. Akkor el kell ismernünk, hogy vannak a világra vonatkozó olyan igazságok, melyeket a tapasztalattól függetlenül tudhatunk;....'' ⁴

A MATEMATIKAI REALISTA MILL nézetei szerint a matematikai és logikai igazságok nem biztosak és nem szükségszerûek, hiszen azok nem mások, mint a világról szerzett empirikus ismereteink legáltalánosabb részei, s mint ilyenek, elvben megdönthetõek.

A LOGIKAI EMPIRISTÁK ezzel szemben nem tagadták a matematikai illetve logikai igazságok szükségszerû és biztos voltát. A probléma megoldását abban látták, hogy a matematikai és logikai igazságok, általában az ,,ész-igazságok'' nem referálnak a világ tényeire. Egy deduktív következtetés során nem tudunk meg többet a világról, mint amit már a premisszákban tudtunk. Tagadják, hogy lennének a priori szintetikus ítéletek.

Popper falszifikácionizmusa szintén elfogadja, hogy a matematikai és logikai iagzságok szükségszerûek és biztosak, s ennek alapján tesz éles különbséget dedukció és indukció között. Hasonlóan, a biztonságos dedukció és a mindig kétséges induktív következtetés közötti különbségtételen alapul a ma legszélesebb körben elfogadott hipotetikus-deduktív, vagy a bayesiánus tudományelmélet, látszólag kiküszöbölve a naiv indukció problémáját.

A RADIKÁLIS FORMALIZMUS alapján az én válaszom az, hogy a matematikai és logikai igazságok nem szükségszerûek illetve nem biztosak, viszont a valóság tényeire reflektálnak. Máris hangsúlyoznom kell azoban, hogy nem úgy, és nem azért, ahogyan ezt például Mill gondolta. Nincs értelme a dedukciónak ugyanis máshol, csak egy formális rendszeren belül. Mint már kifejtettem, minden formális rendszer valóságos fizikai objektumoknak, jeleknek, és valóságos fizikai mûködési mechanizmusoknak, szabályoknak a rendszere. Egy levezetés nem más, mint egy konkrét valóságos fizikai rendszeren végbement folyamat obszervációja . A dedukció kimenetelében csak annyira lehetünk biztosak, mint más fizikai folyamat kimenetelében. Sok olyan, a tapasztalaból indukcióval szerzett tudásunk van, amelyik biztosnak tûnik: Ha egy szûk helyen egy pálcával akarunk valamit kipiszkálni, de a pálca túl hosszú, letörünk belõle, és tudjuk, hogy egy rövidebb pálca lesz a végeredmény. Ennek a mûveletnek a kimenetelében ,,biztosak'' vagyunk. Erre a tapasztalat útján szerzett ismeretre egy majom is rájöhet a pálca használatának próbálgatása közben. Viszont semmivel sem lehetünk biztosabbak abban, hogy az euklideszi axiómákból következik a háromszögekre vonatkozó magasságtétel. A dedukció az indukció egy speciális esete. A formális rendszerre mint fizikai rendszerre vonatkozó tapasztalatból, induktív általánosítás útján nyert ismeret. S mint ilyen, természetesen a valóságos fizikai világ tényeire referál. A formális rendszer maga az a fizikai objektum, amire vonatkozik. Annak a tulajdonságait tükrözi. A magasságtétel igazsága nem azért bizonytalan, mint Mill gondolta, mert a valóságos háromszögek viselkedésében, bármilyen sokszor is teszteljük ezt a viselkedést kísérletileg, nem lehetünk biztosak, hanem azért, mert annak a formális rendszernek viselkedésében, amelynek mûködtetése során a magasságtétel a végeredmény, nem lehetünk biztosak, hiába ismételjük meg a folyamatatot milliószor és milliószor. Az induktív következtetés során elérhetõ bizonyosság a lehetséges bizonyosságok maximuma!

A matematika és a logika tehát empirikus tudományok. A gondolkodás, ha tetszik, egy neurofiziológiai kísérlet. Ha azt a kérdést tesszük fel, van-e olyan sakkjátszma, amelyben a huszadik lépésben négy fekete paraszt a sarokba szorítja a fehér királyt, erre kísérletileg tudunk válaszolni. Induktív következtetés útján szerzett (nem biztos és nem szükségszerû) tudásunk szerint elég egyszer lejátszani egy ilyen menetet, hogy tudjuk, ,,létezik''. Lehet, hogy nem bábukkal játszuk le, hanem papíron, jelekkel. Lehet, hogy nem játsszuk le szó szerinti értelemben, hanem más formális manipulációkat hajtunk végre. Empirikus tudásunk alapján hisszük, hogy egy ilyen átfogalmazás jogos. Tapasztalatunkból kiinduló induktív általánosítások tucatjaira hagyatkozunk a papíron végrehajtott formális manipulációk végrehajtása során. Empirikusan szerzett tudásunk lesz, ha azt vezetjük le, igen, a sakktáblán van olyan játszma, amelynek huszadik lépésében négy fekete paraszt sarokba szorítja a fehér királyt. És ez az állítás a ,,sakk'' nevû formális rendszerre fog vonatkozni. Ez is persze a fizikai valóság egy része. Ebbõl nem következik azonban, hogy az igazi királyt is sarokba szorzíthatja négy fekete paraszt. Hogy ez lehetséges-e, azt a valóságos parasztoknak a valóságos királlyal kell megtapasztalnia.